자기유사성 뜻과 다양한 사례

어릴때 시골에 가서 산에 올라가면 가끔 고사리를 발견하곤 했습니다. 뜯어서 고사리의 형태를 유심히 관찰하면서 아니 어떻게 이렇게 신기하게 생겼지 하면서 계속 멍하니 쳐다봤던 기억이 있는데요. 그러다가 학교에서 고사리의 잎이 프랙탈 구조의 한 예라는 것을 배우게 되었습니다. 또한 잎의 한 부분을 확대해보면 전체의 모양과 비슷한 것을 볼 수 있는데 이 성질을 자기유사성이라고 부른다는 것도 알게 되었습니다. 왠지 모르게 신기하길래 좀더 공부해보았고, 아래에서 자기유사성 뜻과 다양한 사례들에 관해 적어보기로 맘먹었습니다.

자기유사성이란 무엇인가?

자기유사성(self-similarity)은 어떤 물체의 일부분을 확대하거나 축소해서 볼 경우, 그 물체의 전체 형태와 닮은 패턴이 나타나는 성질을 말합니다. 즉 어떤 물체를 다른 배율로 보더라도 형태가 불변하는 성질을 뜻합니다. 그래서 다른 말로 자기 닮음 이라고 부르기도 하는데요.

이 개념을 좀 쉽게 이해하려면 실제 사례들을 보시면 됩니다. 아래 고사리 사진을 보시면 잎의 일부분을 현미경으로 배율을 달리해서 관찰하더라도 형태가 유사한 것을 볼 수 있죠.

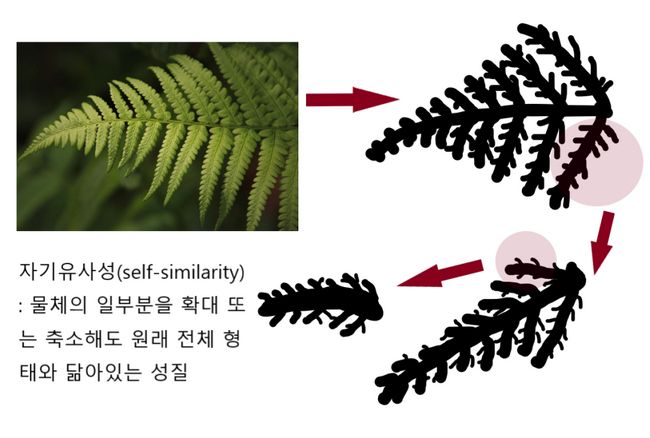
이 자기유사성 개념은 프랑스의 수학자 브누아 망델브로(Benoit Mandelbro, 1924~2010)가 주식시세, 영국의 해안선, 불규칙한 측정값 등을 관찰하다가 발견해낸 것으로 이 발견을 좀더 발전시켜서 프랙탈 이론을 탄생시키게 됩니다.

아마 프랙탈(Fractal)이라는 용어는 많이 들어보셨을텐데요. 이 프랙탈과 자기유사성 개념은 거의 동의어로 쓰이고 있습니다만, 엄밀히 따지면 프랙탈과 자기유사성은 다른 개념으로 볼 수 있습니다.

자기유사성은 부분과 전체가 유사한 형태를 지닌다는 일종의 성질이며, 프랙탈은 이 자기유사성이라는 성질과 함께 순환성이라는 성질도 지닌 기하학적 구조 및 도형을 뜻합니다.

좀더 쉽게 예를 들자면, 우리가 철수라는 사람의 성격을 이야기할때, 친절함, 소심함, 유머러스함 이런식으로 말을 하죠. 여기서 친절하다, 소심하다, 유머러스하다 등의 다양한 성격적 특성중에서 소심함이라는 하나의 성격특성이 자기유사성이라는 성질이라 볼 수 있고, 이러한 다양한 성격을 포함하고 있는 철수라는 사람은 바로 프랙탈이라는 구조나 도형이라고 볼 수 있습니다.

즉 프랙탈이 품고 있는 다양한 특성들 중에 하나가 바로 자기유사성이라는 것입니다. 프랙탈은 자기유사성 말고도 순환성이라는 성질(특성) 또한 지니고 있는데요. 순환성(recursiveness)이란 이러한 자기 닮음 구조가 끊임없이 되풀이 되는 성질을 말합니다.

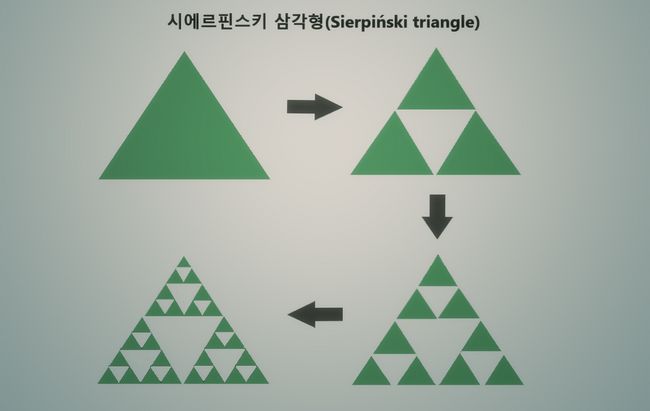
폴란드의 수학자 바츠와프 시에르핀스키의 이름을 딴 시에르핀스키 삼각형(Sierpiński triangle)을 한번 보시죠. 이 프랙탈 도형은 커다란 정삼각형에서 시작해 끊임없이 작은 정삼각형들을 안에 포함하고 있음을 볼 수 있습니다. 이 과정은 무한히 되풀이 된다는 순환성을 지니고 있습니다. 우리 눈에 보이지 않더라도 현미경으로 확대해서 보면 점점 더 작은 정삼각형들로 나눠지는 것을 볼 수 있겠죠.

이 순환성은 코흐 곡선(Koch curve)에서도 볼 수 있습니다. 코흐 곡선은 스웨덴의 수학자 헬게 폰 코흐가 고안한 프랙탈 곡선인데요. 정삼각형을 그린후, 각 변을 3등분해서, 한 변의 길이가 이 3등분의 길이와 같은 정삼각형을 붙입니다.

그리고 이 과정을 무한히 반복하면 코흐 곡선이 탄생하게 되는데, 역시나 자기유사성이 무한하게 반복되는 순환성을 지니고 있음을 알 수 있습니다. 즉 프랙탈은 자기유사성 + 순환성을 지닌 기하학적 구조 및 도형을 뜻하는 개념이고 자기유사성은 하나의 성질을 말하는 것입니다.

그리고 이러한 프랙탈 도형들은 수학자들이 고안해 낸 상상력의 결과물입니다. 반면 현실의 자연에서 발견할 수 있는 프랙탈들은 자기유사성이 무한히 반복되지 않고 몇번 반복하다가 멈추는 것을 관찰할 수 있습니다.

위에서 언급한 고사리의 경우도 잎이 점점 작아지면 어느순간 프랙탈 구조가 아니게 됩니다. 또다른 자연의 프랙탈의 예인 로마네스크 브로콜리도 일정 크기에서는 자기유사성이 반복되지만, 더 작은 부분으로 가면 자기유사성을 잃게 됩니다.

즉 자연속의 프랙탈들은 자기유사성은 지니고 있지만, 자기유사성이 무한히 반복되는 순환성을 지닌 구조는 아니라고 말할 수 있습니다.

아니 그러면 프랙탈은 무한한 재귀성을 지닌 구조인데 그 정의와는 모순이 아니냐? 라고 말하시는 분들이 계실 수 있는데요. 그래서 과학자들중에서는 어떤 구조가 한 100배, 1000배 확대할때까지는 자기유사성을 띄고 있으면 프랙탈로 부르자고 말하기도 합니다.

아무튼 자연속에서 프랙탈로 불리는 물체들은 10배~100배정도까지 확대할때까지만 자기유사성을 지닌 경우가 많고, 그 이상 확대하면 자기유사성을 잃는 경우가 많기 때문에, 망델브로의 정의에 따르면 프랙탈로 부르기 애매하다고 볼 수 있습니다. 아마도 진정한 프랙탈은 현실에서 찾아보기 힘들고, 수학적 상상력으로만 존재하는 것일 수도 있습니다. 물론 우리들은 편의상 자연속에서 어느정도의 자기유사성만 지니고 있어도 프랙탈로 부르고 있지만, 그것은 불완전한 프랙탈이라고 볼수 있겠습니다.

또한 수학에서는 이러한 자기유사성을 강도에 따라 3가지 유형으로 구분하기도 하는데요. 즉 부분이 전체를 닮기는 하는데 복사붙여넣기 한것처럼 완전히 똑같이 닮는지, 아니면 형태가 불완전하게 닮는지 그 강도에 따라 분류하는 것입니다.

• 정확한 자기유사성(Exact self-similarity) – 시에르핀스키 삼각형이나 코흐 곡선처럼 자기 유사성의 강도가 가장 높은 것으로 부분과 전체의 모양이 정확하게 같습니다.

• 준-자기유사성(Quasi-self-similarity) – 어느정도 느슨한 형태의 자기유사성을 띄는 것으로 형태가 정확하게 일치하지 않고 어느정도 왜곡되고 변형되어 있습니다.

• 통계적 자기유사성(Statistical self-similarity) – 자기유사성의 강도가 가장 약한 것으로 자연에서 발견되는 프랙탈처럼 부분과 전체가 대략적으로 비슷한 형태를 보입니다.

아무튼 위에서 적은 내용들을 바탕으로 하자면, 자연에서 관찰되는 프랙탈들은 자기유사성이 무한히 반복되는 것도 아니고, 그 강도(닮은 정도)도 가장 약한 물체들이라고 볼 수 있겠습니다.

자연의 물체들이 자기유사성을 띄는 이유는 뭘까?

그렇다면 대체 자연에서 수많은 프랙탈들이 관찰되는 이유는 뭘까요? 고사리의 잎이나 브로콜리나, 인간의 폐의 형태 등 자연의 물체들은 왜 자기유사성을 띄려고 노력하는 걸까요? 저는 이 부분이 가장 궁금했습니다.

그저 유전자에 각인된 신의 설계도에 따라 자기를 완성시키려는 것 뿐일까..우연하게 저런 구조를 발견했고, 그게 현실의 생존에 가장 유리했기 때문일까..그러면 생물이 아닌 무생물들. 해안선이나 구름, 번개 이런 우주의 수많은 물체나 자연현상들까지도 자기 유사성을 띄는건 왜일까? 그리고 이러한 자기유사성이 불가능한게 아니라 가능한 이유는 무엇일까…아무튼 밤에 산책을 하면서 혼자 나름 열심히 고민을 해봤지만, 역시나 뾰족한 답을 얻을 수 없었습니다. 뭐 그렇죠..뭐..

이 물음에 대해서 수학자들은 이런 해답을 내놓습니다. 그것은 바로 프랙탈 구조는 작은 공간을 효율적으로 사용해서 표면적(물체 겉면의 넓이)를 넓힌다는 것입니다.

예를 들어 폐는 산소와 이산화탄소를 교환해주는 역할을 하는 기관으로 자기유사성을 지닌 프랙탈인데요. 폐 속에는 폐포라고 부르는 작은 기관이 무수히 많아서 동일한 부피에서 표면적을 넓혀서 산소와 이산화탄소의 교환을 좀더 효율적으로 할 수 있게 해준다는 것입니다.

또한 소장의 융털 또한 소장의 표면적을 넓혀줌으로써 섭취한 음식물의 영양분을 더욱 효율적으로 흡수하게 만들어 줍니다.

그리고 인간의 뇌 또한 작은 공간속에 수많은 주름으로 뇌세포를 더 많이 배치할 수 있어서 프랙탈 구조를 하는 것이 더욱 효율적이라는 것입니다.

즉 수학자들은 최소비용으로 최대 효과를 내는 효율성이 자기유사성의 비밀이라고 해답을 내놓았네요. 그러고보면 이 세상은 무한한 공급이란 없는 차가운 현실인가 봅니다. 현실의 공간과 시간, 자원은 항상 부족하기에, 자연의 수많은 것들은 치열하게 효율성을 추구하려고 연구하나 봅니다.

그리고 저는 또다른게 궁금해지더군요. 프랙탈은 눈에 보이는 형태가 자기유사성을 띄며 반복되는 것인데, 이것이 표면적을 넓히는 효율성을 추구하기 위한 것이라면 그렇다면 우리 눈에 보이지 않는 것. 이를테면 관념, 정신활동 같은 것은 효율성을 추구하려 하지 않을까? 하는 생각이 들었습니다. 과연 현실에서 공간을 점유하지 않는 것들도 효율성을 추구하려 할까? 만약 그렇다면 그것들에게는 어떤 방식이 가장 효율적일까? 뭐 이런 고민을 했습니다.

자기유사성 사례

수학적 상상력으로 만들어낸 자기유사적 프랙탈들은 망델브로 집합, 코흐곡선(코흐 눈송이), 시에르핀스키 삼각형, 쥘리아 집합, 하우스도르프 차원, 칸토르 집합, 멩거 스펀지 등이 있습니다.

자연속에서 발견할 수 있는 자기유사성의 사례로는 로마네스크 브로콜리, 나뭇잎의 정맥, 공작 깃털, 인터넷 네트워크망, 전화선, 상하수도관, 눈송이, 뇌의 신경세포, 은하와 허리케인, 번개, 해안선, 노틸러스 껍질, 뭉게구름, 고사리와 같은 양치류 식물, 하천의 흐름, 산맥의 지형, 동물의 혈관, , 나뭇가지의 모양 등이 있습니다.

위에서도 언급했듯이 자연에서 발견되는 물체들은 자기유사성이 무한히 반복되지 않고, 어느정도만 반복되는 경향을 보입니다. 또한 완전히 판박이처럼 빼닮는게 아니라, 어느정도 닮은 형태를 띄고 있는 것을 볼 수 있습니다.

또한 이러한 자기유사성은 현실에서 작은 공간내에서 표면적을 가장 넓히기 위한 효율성을 치열하게 추구한 결과물이라고 수학자들은 말합니다. 정말 자연은 신비스러우면서도 대단하기도 하고, 한편으로는 얼마나 수많은 수학적 비밀들이 숨겨져 있는지 무섭기까지 하네요.